
Der Fluch von Martingale
Sind Banker Parasiten?
Aus der linken Ecke kommt seit geraumer Zeit die Behauptung, die Finanzindustrie würde sich nahezu parasitär von der "Realwirtschaft" ernähren.
Eine Erklärung, warum diese Beziehung eher eine Symbiose ist, liefert der "Fluch von Martingale". Dieses Konzept ist nicht ganz trivial zu verstehen, aber es hat ausgesprochen reale Konsequenzen.
Doch genauso faszinierend ist, dass dieses Konzept so oft und konsequent falsch verstanden wird. In diesem Artikel werde ich versuchen, das Konzept anhand von einfachen Überlegungen und Simulationen darzustellen.
Kopf oder Zahl?
Münzen werden in der Mathematik eigentlich schon oft genug missbraucht, aber ich muss nun trotzdem ein einfaches Münzspiel bemühen um ein paar wichtige Punkte zu erläutern.
Der Spieler bekommt ein Startkapital. Sagen wir 100€. In jeder Runde kann er einen beliebigen Anteil (kleiner oder gleich 100%) seines Kapitals setzen, mit beliebiger Genauigkeit (zum Beispiel 0,000001€). In jeder Runde wird eine Münze geworfen, bei Zahl verliert der Spieler den Einsatz, bei Kopf gewinnt er 150% des Einsatzes. Hat der Spieler weniger als einen Euro übrig, gilt er als Pleite und bleibt bei diesem Kapital stehen.
Der zu erwartende Gewinn wäre also 25% des Einsatzes pro Runde, weil entweder 100% verloren gehen oder 150% hinzu kommen, also ist der Durchschnitt (-100+150)/2 also 25%.
Eigentlich ein sehr guter Deal oder? Witzigerweise, wenn man dieses Spiel von Probanden spielen lässt, gehen die meisten Spieler Pleite.
Versuch es selbst!
Wie Du vielleicht festgestellt hast, ist die beste Strategie, einen kleinen Anteil des aktuellen Kapitals zu setzen. Zum Beispiel 10%. Das bedeutet, dass nach Verlusten der Einsatz sinkt und nach Gewinnen der Einsatz steigen sollte. Bei konstantem Einsatz bleibt das Kapital entweder zu flach (wenn der Einsatz zu klein ist) oder man geht Pleite (wenn der Einsatz zu hoch ist, zum Beispiel 50€).
Hier ein Diagramm wie ein einzelner Durchgang aussehen kann mit einer konstanten Strategie:
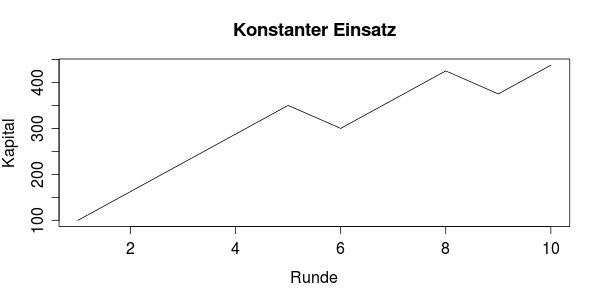
Wie man sieht, geht es stetig nach oben mit ein paar Aussetzern. Natürlich ist das nur eine der 210 verschiedenen Möglichkeiten!
Man kann jetzt zwar mathematisch beweisen, wie die Verteilung der Gewinne aussieht, aber eine Simulation tut es auch. Dann ergibt sich folgendes Histogramm, also eine Verteilung der möglichen Gewinne:
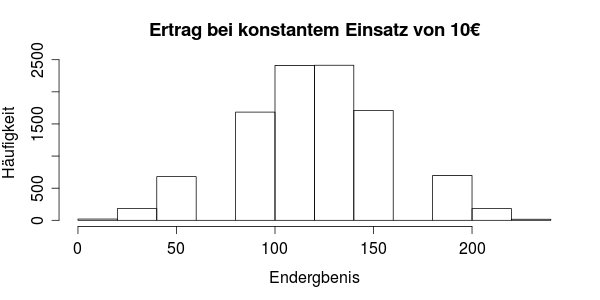
In diesem Fall erhalten wir in der Simulation einen Durchschnitt von 122€ als Endkapital. Das entspricht in etwa unserer Erwartung von 125€. Obwohl das Spiel für den Spieler extrem positiv ist, bringen 25% Der Durchgänge einen Verlust ins Ziel. Das ist das Problem mit sogenannten stochastischen Entwicklungen: Es gibt zwar eine hübsche mathematische Erklärung für einen satten Gewinn im "Durchschnitt", aber man hat nur eine endlich Anzahl von Versuchen, und dabei kann einiges schief gehen.
Nochmal dasselbe mit einem konstanten Einsatz von 20€:
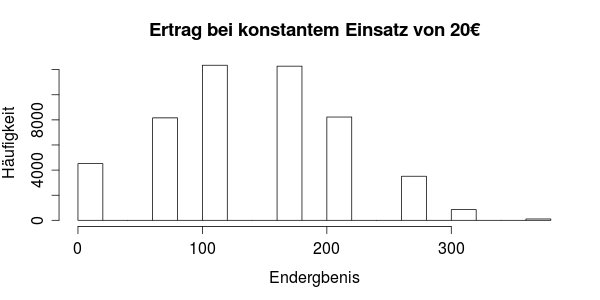
Der Plot sieht etwas anders aus als der Erste. Die Säulen sind deshalb so weit auseinander, weil es nur wenige mögliche Endergebnisse in dieser Simulation gibt und ein Spieler für Pleite erklärt wird sobald er einen oder weniger Euro erreicht.
In diesem Fall haben ebenfalls 25% der Spieler einen Verlust eingefahren. Und 3,5 % sind sogar Pleite. Trotz des eigentlich enorm positiven Spiels!
Und noch merkwürdiger: Der Durchschnitt liegt bei 145€, trotz der vielen Pleitegeier, ist also höher als bei der Strategie mit weniger Einsatz. Auch so eine Nebenwirkung vieler stochastischer Prozesse: Die Strategie kann fast jeden ruinieren und trotzdem im Schnitt super aussehen.
Wie schon angedeutet, ist ein prozentualer Wetteinsatz besser. Sagen wir mal wir setzen immer 10% des Kapitals. Dann erhalten wir die folgende Verteilung:
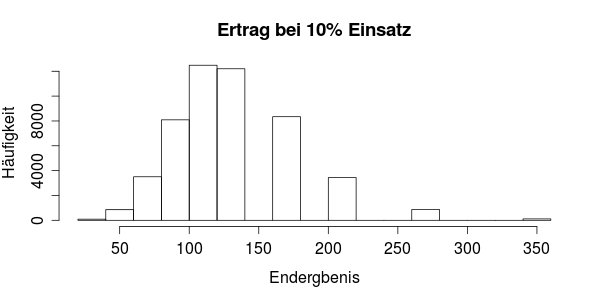
Da 10% von 100€ genau 10€ sind, ist die Verteilung recht ähnlich zum Histogramm für einen konstanten Einsatz von 10€. Der Durchschnitt liegt bei 125€ und 25% der Spieler verlieren Geld.
Allerdings sieht die Verteilung etwas anders aus. Der Grund dafür ist, dass diese Strategie exponentiell wächst und daher höhere Gewinne möglich sind, während höhere Verluste eher seltener werden.
So langsam sollte der Groschen fallen, dass weniger durchaus mehr ist, und dass der Ertrag zwar mit steigendem Risiko steigt, auch im Durchschnitt, aber auch die Verlustwahrscheinlichkeit geht ebenfalls rasant nach oben.
Hier mal eine Kurve aus Simulationen für eine Reihe von prozentualen Einsätzen:
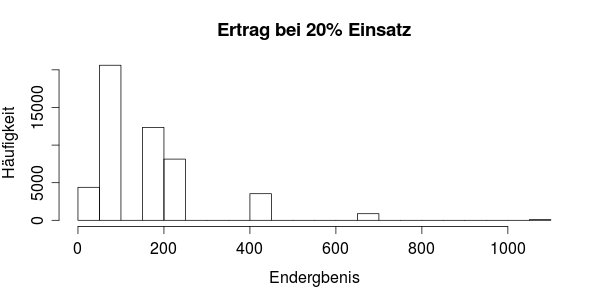
Hier sehen wir, dass mit 20% Einsatz noch höhere Gewinne möglich sind. in diesem Fall liegt der Durchschnitt bei 155€. Allerdings liegen 50% der Durchläufe unter 100€. Angenommen man kann dieses Spiel nur einmal im Leben spielen, wäre das nicht akzeptabel.
Also hängt sowohl der Gewinn, als auch das gesamte Verlustrisiko davon ab:
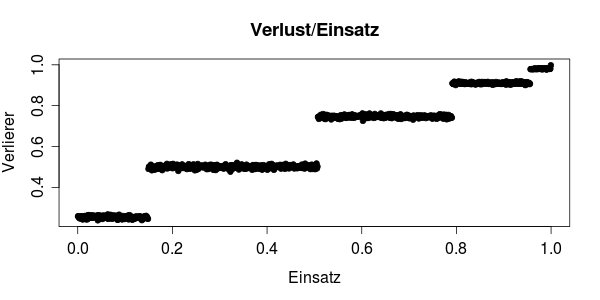
Je höher der Einsatz der Strategie, desto wahrscheinlicher führt sie in den Ruin. In dieser Grafik gibt es Stufen, da ich nur 10 Runden pro Durchgang simuliere.
Die Martingale Eigenschaft
Das Problem mit diesen Wachstumsstrategien ist, dass sie sehr anfällig für Rückschläge sind. Wann immer das Kapital unter einer Pechsträhne leidet, muss die Wachstumskurve "von vorne" beginnen, egal wie hoch das Kapital vorher gestiegen war. Etwas deutlicher ist dieser Effekt in dieser Grafik zu sehen:
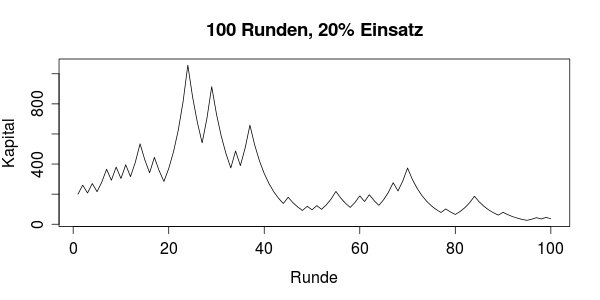
In dieser Kurve sehen wir mindestens zwei mal die Ansätze von exponentiellem Wachstum nach einem Rückschlag. Jedes mal muss die Kurve mit geringem (absolutem) Wachstum anfangen. Und der Effekt ist dramatisch: Statt einer netten exponentiellen Gewinnkurve stagniert das Kapital auf niedrigem Niveau.
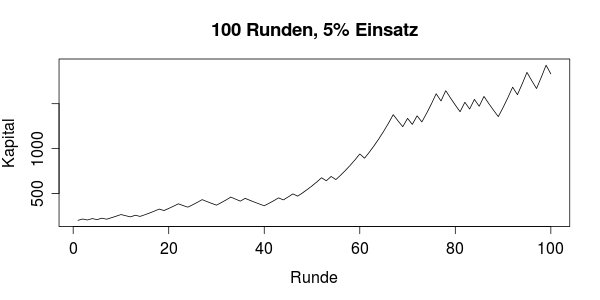
Und genau das bezeichne ich als den Fluch von Martingale. Zu viel Einsatz, und die Wachstumskurve stagniert. Zu wenig Einsatz und das Wachstum kommt ebenfalls nicht in Schwung.
Spieler in Glücksspielen oder auch manche Aktienhändler ignorieren die Martingaleeigenschaft. Aus welcher Begründung auch immer glauben sie, nach Verlusten ein wesentlich steileres Wachstum "verdient" zu haben. Also setzen sie mehr, und verlieren unter Umständen noch mehr.
Konsequenzen
Dieses Münzspiel ist relativ simpel, wir kennen die Wahrscheinlichkeiten exakt, und daher können wir mit Simulationen oder auch Mathematik herausfinden, welcher Einsatz der richtige für uns ist.
In der Wirtschaft ist es natürlich komplizierter. Aber auch hier müssen Entscheidungen getroffen werden, wieviel Kapital oder Energie für die verschiedensten Unternehmungen "riskiert" werden soll.
Essentiell für diese Entscheidungen ist, das Spiel zu kennen, also Gewinn und Risiko zu beurteilen. Die Finanzindustrie übernimmt genau diese Aufgabe. Sie analysiert die "Spiele" und setzt das Kapital so ein, dass möglichst eine Wachstumskurve entsteht.
Der Unterschied im Wirtschaftswachstum zwischen einer Gesellschaft mit funktionierender Finanzindustrie und einer Gesellschaft ohne eine kompetente Risikobewertung ist extrem dramatisch. Und dementsprechend wirkt es nicht mehr so "blutsaugend", wenn die Finanzindustrie einen nicht gerade kleinen Anteil dieses Vorteils verschlingt.
"Riskieren" klingt in diesem Zusammenhang recht freiwillig. Aber Unsicherheit ist schließlich überall. Wenn ich mein Auto korrekt parke, geh ich immer noch das Risiko ein, dass es von einem anderen Auto gerammt wird.
Selbst ein einfacher Bauer muss Risikobewertung betreiben. Wenn er Getreide erntet, dann wird er einen Teil davon lagern, einen Teil verkaufen und einen Teil in die nächste Aussaat investieren. Allerdings durch Wetter und Schädlinge riskiert er, einen Teil oder sogar die gesamte nächste Ernte zu verlieren.
Oligarchien leben gefährlich
Eine andere Konsequenz ist: Je mehr Risiko, desto schlimmer schlägt der Fluch von Martingale zu.
Wenn eine Gesellschaft zu viel auf die Entscheidung eines einzigen egal wie kompetenten Fachmannes setzt, riskiert sie regelmäßige herbe Rückschläge und eine entsprechende Stagnation.
1958 rief Mao Ze Dong in der Volksrepublik China unter anderem die Kampagne "Ausrottung der vier Plagen" ins Leben. Eine dieser Plagen waren Sperlinge. In ganz China, und China ist wirklich kein kleines Land, wurde nun Jagd auf Sperlinge gemacht. Doch die Sperlinge sind eher Nützlinge als Schädlinge, und die folgenden Insektenplagen trugen zu einer der größten Hungersnöte der Menschheitsgeschichte bei.
Das ist ein trauriges Beispiel dafür, zu viel auf eine Idee zu setzen, egal wie logisch sie anfangs auch klingen mag.
blog comments powered by Disqus